MODELO GRAFICO
Como es de esperar, el método grafico consiste en representar las gráficas asociadas a las ecuaciones del sistema para deducir su solución. La solución del sistema es el punto de intersección entre las gráficas. La razón de ello es que las coordenadas de dicho punto cumplen ambas ecuaciones y, por tanto, es la solución del sistema.
Como vamos a trabajar con sistemas de dos ecuaciones lineales con dos incógnitas (x e y), la gráfica de cada ecuación es una recta. Como consecuencia, la intersección de las gráficas es un único punto (a, b)
y la solución del sistema es x = a e y = b. No obstante, si las rectas son paralelas (no se cortan), el sistema no tiene solución, y si son iguales hay infinitas soluciones.
Los pasos necesarios para realizar el método son siete:
1. graficar las soluciones factibles, o el espacio de soluciones
(factible), que satisfagan todas las restricciones en forma simultánea.
2. Las restricciones de no negatividad Xi>= 0 confían todos los valores posibles.
3. El espacio encerrado por las restricciones restantes se determinan sustituyendo en primer término <= por (=) para cada restricción, con lo cual se produce la ecuación de una línea recta.
4. trazar cada línea recta en el plano y la región en cual se encuentra cada restricción cuando se considera la desigualdad lo indica la dirección de la flecha situada sobre la línea recta asociada.
5. Cada punto contenido o situado en la frontera del espacio de soluciones satisfacen todas las restricciones y por consiguiente, representa un punto factible.
6. Aunque hay un número infinito de puntos factibles en el espacio de soluciones, la solución óptima puede determinarse al observar la dirección en la cual aumenta la función objetivo.
7. Las líneas paralelas que representan la función objetivo se trazan mediante la asignación de valores arbitrarios a fin de determinar la pendiente y la dirección en la cual crece o decrece el valor de la función objetivo.
2. Las restricciones de no negatividad Xi>= 0 confían todos los valores posibles.
3. El espacio encerrado por las restricciones restantes se determinan sustituyendo en primer término <= por (=) para cada restricción, con lo cual se produce la ecuación de una línea recta.
4. trazar cada línea recta en el plano y la región en cual se encuentra cada restricción cuando se considera la desigualdad lo indica la dirección de la flecha situada sobre la línea recta asociada.
5. Cada punto contenido o situado en la frontera del espacio de soluciones satisfacen todas las restricciones y por consiguiente, representa un punto factible.
6. Aunque hay un número infinito de puntos factibles en el espacio de soluciones, la solución óptima puede determinarse al observar la dirección en la cual aumenta la función objetivo.
7. Las líneas paralelas que representan la función objetivo se trazan mediante la asignación de valores arbitrarios a fin de determinar la pendiente y la dirección en la cual crece o decrece el valor de la función objetivo.
Ejemplo
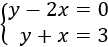
Resolución:
Lo primero que hacemos es despejar la y en ambas ecuaciones.
Primera ecuación:
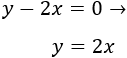
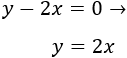
Segunda ecuación:
Ahora vamos a calcular unos cuantos puntos de las dos funciones para representarlas. Utilizamos, por ejemplo, x = 0 y x = 2.
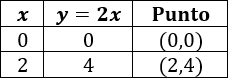
Para la primera función tenemos la tabla
Para la segunda función tenemos la tabla (utilizando los mismos valores para x):
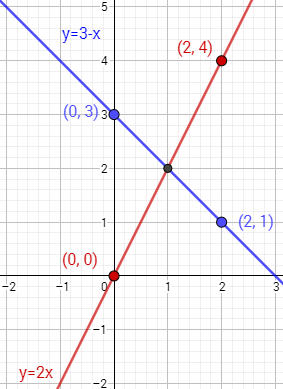
Representamos los puntos de las tablas y los unimos:
La solución del sistema es el punto donde las gráficas se cortan:
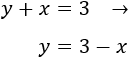
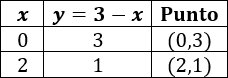
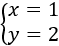
No hay comentarios:
Publicar un comentario