FORMA GENERAL DE LA FUNCIÓN EXPONENCIAL

       

FORMA GENERAL DE LA FUNCION EXPONENCIAL


Las funciones exponenciales tienen la forma f(x) = bx, donde b > 0 y b ≠ 1. Al igual que cualquier expresión exponencial, b se llama base y x se llama exponente.


las funciones exponenciales se caracterizan únicamente por el hecho de que la tasa de crecimiento de dicha función (es decir, su derivada) es directamente proporcional al valor de la función. La constante de proporcionalidad de esta relación es el logaritmo natural de la base b:




Las funciones de crecimiento exponencial son supuestas porque el valor de una función de crecimiento exponencial aumenta siempre. Las funciones de crecimiento exponencial se utilizan para modelar el crecimiento demográfico. Una función exponencial puede modelar exactamente el crecimiento demográfico donde la disponibilidad de recursos no limita excesivamente el crecimiento.


función exponencial exige que la base sea siempre positiva y diferente de uno (b 0 y b≠1). La condición que b sea diferente de uno se impone, debido a que al reemplazar a b por 1, la función bx se transforma en la función constante f(x) = 1. La base no puede ser negativa porque funciones de la forma f(x)=(-9)1/2 no tendrían sentido en los números reales.


Ejemplo:




Problema


Hacer una tabla de valores para f(x) = 3x.









x


f(x)






















Has una “T” para empezar la tabla con dos columnas. Etiqueta las columnas con x y f(x).









x


f(x)



−2







−1







0







1







2








Escoge varios valores para x y ponlos como filas separadas en la columna x.






Consejo: Siempre es bueno incluir el 0, valores positivos y valores negativos, si es posible.



Respuesta




x


f(x)



−2






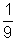
−1






0


1



1


3



2


9




Evalúa la función para cada valor de x y escribe el resultado en la columna f(x) junto al valor de xcorrespondiente. Por ejemplo, cuando x = −2, f(x) = 3-2 = 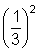= 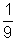, entonces 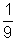va en la columna f(x) junto al −2 de la columna x. f(1) = 31 = 3 y 3 va en la columna f(x) junto al 1 de la columna x.






Observa que tu tabla de valores podría ser distinta a la de alguien más, si escogiste diferentes números para x.





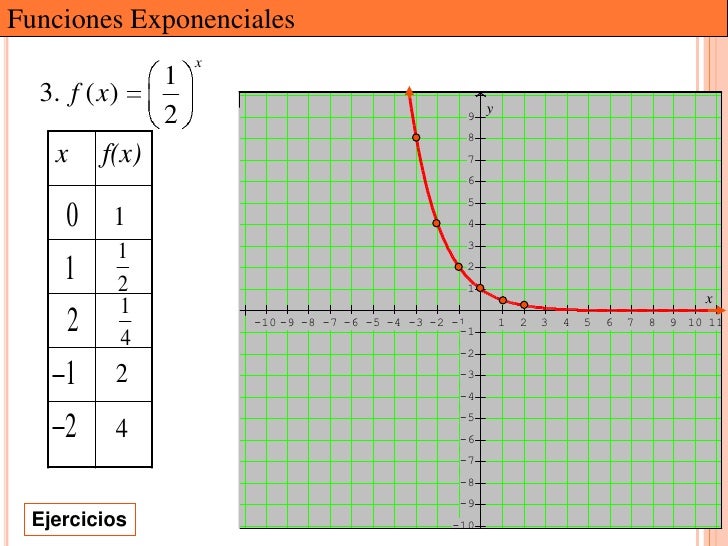
Imagen:






Video: