GRAFICACIÓN DE FUNCIONES

FUNCIONES ESPECIALES

FUNCIÓN ESCALONADA

Es aquella cuya grafica esta formada por segmentos de rectas horizontales parecidos a escalones.

 El ejemplo más común de función escalonada es la función parte entera. Otras funciones escalonadas son la función unitaria de Heaviside o función escalón unitario, y la función signo. 

Como caso general podemos ver la función y = s(x), definida así:

En el intervalo cerrado [-1, 5] de números reales sobre los números reales, asociando a cada x de [-1,5] un valor de y, según el siguiente criterio:

Esta función tiene cuatro intervalos escalonados, como se ve en la figura.
La composición de cualquier función escalonada s(x) y una función cualquiera f(x) da por resultado una función escalonada g(x) = f(s(x)), siempre que f(x) esté definida para cualquier valor de x en el rango de s(x).
Evidentemente, la derivada de una función escalonada es 0 en cualquier punto en que se halle definida. No puede definirse en los puntos en que hay discontinuidades.

EJEMPLO:

FUNCIÓN VALOR ABSOLUTO

Es aquella que asocia cada numero real con su valor absoluto, es decir, asocia cada numero con su valor sin signo.

La regla de asociación es la siguiente:

Generalmente el valor absoluto se representa por |x|. Si desarrollamos una tabla de valores

Gráficamente obtenemos lo siguiente: 

Las caracteristicas más importantes de esta funcion son:

a) La gráfica esta formada por dos ramas lineales simétricas

b) Las ramas linealesde la gráfica forman un ángulo de 45° con los ejes.

c) Esta gráfica tine forma de ''V'' 

En cuanto al dominio y el rango: 

• EL DOMINIO: esta formado por todos los números reales pues no hay restricciones en esta función. 
• EL RANGO: esta conformado por todos los números reales positivos
  [0, ∞) 

FUNCIÓN IDENTIDAD 

Esta relacionada cada elemento del dominio con su igual en el codominio

f(x) = x

La identidad es una función lineal de pendiente m = 1 que pasa por el origen de coordenadas, es decir, por el punto (0,0). Divide el primer y el tercer cuadrante en partes iguales, o sea, es su bisectriz.

La pendiente es la inclinación con respecto al eje X (eje de abscisas). Al ser ésta positiva (m > 0), la función es creciente.

Que la pendiente de la función identidad sea m = 1 significa que si aumentamos la x en una unidad, la y también aumenta en una unidad.

Formará un ángulo de 45° con cualquiera de los ejes.

La identidad id es el elemento neutro en la composición de funciones. Es decir, cualquier función f compuesta con la identidad es ella misma.

Las caracteristicas más importantes de esta función son: 

a) Su gráfica siempre es una línea recta que forma un angulo de 45° con los ejes. 

b) Es una gráfica que siempre cruza el origen

Respecto al dominio y rango tenemos las siguientes conclusiones: 

• El dominio son  todos los numeros reales, ya que la función no marca ninguna restricción
• El rango esta formado por los mismos elementos que el dominio. 

FUNCIÓN CONSTANTE

Es aquella que relaciona todos los elementos del dominio con un solo elemento del codominio. Este elemento generalmente es una constante: 

EJEMPLO: 

Caracteristicas que identifican esta funcion: 

a) Su gráfica generalmente es una recta paralela al eje x

b) Siempre corta al eje y en la constante que marca la función

c) es una gráfica simétrica respecto al eje de y, es decir, que este ultimo se comporta como un espejo de la función

Respecto al dominio y rango tenemos las siguientes conclusiones: 

• El dominio son todos los numeros reales ya que la función no tiene restricción alguna 
• El rango esta formado por un solo elemento: la constante expresada en la función.

FUNCIÓN INYECTIVA (UNO A UNO) 

Sea f función de A en B, entonces es inyectiva si y solo si elementos distintos de A, les hace corresponder imágenes distintas en B, es deir, que ningún elemento de A tiene la misma imágen. 

f es inyectia si se cumple f(x) =f (y) solo cuando x = y 

EJEMPLO: 

FUNCIÓN SOBREYECTIVA

Sea f una función de A en B, entonces f es sobreyectiva si y solo si cada elemento de B es imagen de al menos un elemento de A, o sea que todos los elementos de B estan asociados con por lo menos uno de A, es decir: 

f es sobreyectiva si se cumple que rango de f = B

FUNCIÓN BIYECTIVA 

Sea función de A en B, entoonces f es biyectiva solo si f es inyectiva y sobreyectiva a la vez, es decir, cada elemento de B es imágen  de uno y solo un elemento de A

f es biyectiva si se cumple que f es sobreyectiva y f es inyectiva

EJEMPLO: 

FUNCIÓN INVERSA

Se llama función inversa o recíproca de una función f a una nueva función cuyo dominio es la imagen de la función inicial, y su imagen es el dominio de la función inicial.

Es decir, si la función g es la función inversa de f, entonces se cumple que si f (b) = a, entonces g(a)=b.


1. Si realizamos la función inversa de una composición de funciones obtenemos la composición de sus inversas permutando el orden de la composición:



2. Si hacemos la inversa de una función , obtenemos la función inicial



3. La composición de una función y su inversa nos da la función identidad.
4. La función inversa no siempre existe.
5. Si una función es continua también lo es su inversa y viceversa, si la inversa es derivable también lo será la función inicial.
6. Análogamente, si una función es derivable su inversa también lo es y viceversa.

GRÁFICA DE UNA FUNCIÓN INVERSA

La gráfica de una función f, y la de su inversa g, son simétricas respecto a la bisectriz del primer y tercer cuadrante, es decir la recta y = x, como podemos ver en la siguiente imagen:

Por tanto si M(b,a) es un punto de f, y por tanto sabemos que M´(a,b) será un punto de g, entonces las pendientes de las tangentes en M y en M´son inversas. Es decir si la pendiente de la tangente en M es m, entonces la pendiente de la tangente en M´ será 1/m.



El ejemplo más conocido e importante de funciones inversas es la función exponencial y la función logarítmica. Y como podemos ver sus representaciones gráficas son simétricos respecto de la bisectriz del primer y tercer cuadrante:








CALCULAR FUNCIÓN INVERSA
1. Realizamos un cambio de variable, cambiando y por x, y viceversa.
2. Despejar la variable y en función de x.
3. El resultado final, es la función inversa que hemos buscado.

EJEMPLO:



Calcular la siguiente función inversa:

1. Hacemos el cambio de y por x:

2. Despejamos la y:

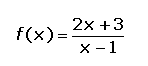
3. La función inversa es:

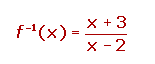
FUNCIÓN CRECIENTE Y DECRECIENTE  

CRECIENTE
 Son aquellas que cumplen las siguientes condiciones:
si los valores del dominio aumentan, entonces se observa que las imágenes correspondientes crecen

EJEMPLO:

Las funciones decrecientes son aquellas que cumplen la siguiente condición: si los elementos del dominio aumentan entonces las imágenes correcpondientes decrecen o disminuyen 

EJEMPLO: