Una función polinomial es una función cuya regla esta dada por un polinomio en una variable. El grado de una función polinomial es el grado del polinomio en una variable, es decir, la potencia mas alta que aparece de x.
http://www.unl.edu.ar/ingreso/cursos/matematica/wp-content/uploads/sites/7/2017/07/M%C3%B3dulo-7-Funciones-polinomiales.pdf
FUNCIÓN LINEAL
Una función lineal es una función polinómica de grado 1 que pasa por el origen de coordenadas, es decir, por el punto (0,0). Son funciones rectas de la forma:


La m es la pendiente de la recta. La pendiente es la inclinación con respecto al eje X (eje de abscisas). Si m es positiva (m > 0), entonces la función es creciente. En cambio, si la m es negativa (m < 0), entonces la función es decreciente.
La pendiente m significa que si aumentamos la x en una unidad, la y aumenta en m unidades. Si la m es positiva, según aumente la x la y también irá aumentando (función creciente). En cambio, si m es negativa, cuando aumenta la x la y disminuirá (función decreciente).
Ejercicio
Sea una función f(x) = 2x. El escalar m es el coeficiente que multiplica a la x, o sea m = 2.
La función es lineal ya que pasa por el punto (0,0), el origen.
La pendiente de la recta de la función es positiva (m = 2), por lo tanto, la función es creciente.
Función identidad
Una función identidad es una función tal que la imagen de cualquier elemento es éste mismo:

La función identidad también suele denotarse por id.

METODO GRAFICO
Cada una de las ecuaciones que forman un sistema lineal de dos ecuaciones con dos incógnitas es la de una función de primer grado, es decir, una recta. El método gráfico para resolver este tipo de sistemas consiste, por tanto, en representar en unos ejes cartesianos, o sistema de coordenadas, ambas rectas y comprobar si se cortan y, si es así, dónde. Esta última afirmación contiene la filosofía del proceso de discusión de un sistema por el método gráfico. Hay que tener en cuenta, que, en el plano, dos rectas sólo pueden tener tres posiciones relativas (entre sí): se cortan en un punto, son paralelas o son coincidentes (la misma recta). Si las dos rectas se cortan en un punto, las coordenadas de éste son el par (x, y) que conforman la única solución del sistema, ya que son los únicos valores de ambas incógnitas que satisfacen las dos ecuaciones del sistema, por lo tanto, el mismo es compatible determinado. Si las dos rectas son paralelas, no tienen ningún punto en común, por lo que no hay ningún par de números que representen a un punto que esté en ambas rectas, es decir, que satisfaga las dos ecuaciones del sistema a la vez, por lo que éste será incompatible, o sea sin solución. Por último, si ambas rectas son coincidentes, hay infinitos puntos que pertenecen a ambas, lo cual nos indica que hay infinitas soluciones del sistema (todos los puntos de las rectas), luego éste será compatible indeterminado.
El proceso de resolución de un sistema de ecuaciones mediante el método gráfico se resume en las siguientes fases:
Se despeja la incógnita y en ambas ecuaciones.
Se construye, para cada una de las dos funciones de primer grado obtenidas, la tabla de valores correspondientes.
Se representan gráficamente ambas rectas en los ejes coordenados.
En este último paso hay tres posibilidades:
Si ambas rectas se cortan, las coordenadas del punto de corte son los únicos valores de las incógnitas x e y. Sistema compatible determinado.
Si ambas rectas son coincidentes, el sistema tiene infinitas soluciones que son las respectivas coordenadas de todos los puntos de esa recta en la que coinciden ambas. Sistema compatible indeterminado.
Si ambas rectas son paralelas, el sistema no tiene solución. Sistema incompatible.
Veamos, por última vez, el ejemplo visto en los métodos analíticos para resolverlo gráficamente y comprobar que tiene, se use el método que se use, la misma solución. recordemos de nuevo el enunciado:
Entre Ana y Sergio tienen 600 euros, pero Sergio tiene el doble de euros que Ana. ¿Cuánto dinero tiene cada uno?.
Llamemos x al número de euros de Ana e y al de Sergio. Vamos a expresar las condiciones del problema mediante ecuaciones: Si los dos tienen 600 euros, esto nos proporciona la ecuación x + y = 600. Si Sergio tiene el doble de euros que Ana, tendremos que y = 2x. Ambas ecuaciones juntas forman el siguiente sistema: x + y = 600 2x - y = 0
Para resolver el sistema por el método gráfico despejamos la incógnita y en ambas ecuaciones y tendremos: y = -x + 600 y = 2x
Vamos ahora, para poder representar ambas rectas, a calcular sus tablas de valores:
y = -x + 600 y = 2x
x y x y
200 400 100 200
600 0 200 400
Con estas tablas de valores para las dos rectas y eligiendo las escalas apropiadas en los ejes OX y OY, podemos ya representar gráficamente:

Si observamos la gráfica, vemos claramente que las dos rectas se cortan en el punto (200, 400), luego la solución del sistema es x = 200 e y = 400. Por tanto, la respuesta al problema planteado es que Ana tiene 200 euros y Sergio tiene 400 euros, es decir, el mismo resultado, evidentemente, que habíamos obtenido con los tres métodos analíticos.
Raíz de una función lineal
La raíz (x1) de una función lineal es el valor de x que se corresponde con el valor de ordenada cero, es decir, (x1, 0).
Para que un número sea raíz de una función debe cumplirse que:
ƒ: R → R tak que ƒ(x) = mx + b, con m ≠ 0 si y sólo si ƒ(x1) = 0
Estudiemos un ejemplo de análisis de función lineal para aclarar los conceptos antes mencionados.
Ejercicio: Calcular la raíz, indicar la ordenada al origen y pendiente de la recta: y = 3x+6. Graficar.
Utilizamos la ecuación de la recta para determinar cuál es la ordenada al origen y la pendiente.
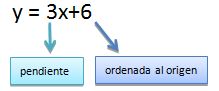
m = 3
b = 6
Cálculo de la raíz
y = 3x+6
Reemplazamos a la y, por 0:
0 = 3x + 6
Despejamos la x:
-6 = 3x
-6/3 = x
x = -2 - Raíz de la función
Con estos datos podemos graficar. Ubicamos el punto de la raíz, el de la ordenada al origen y luego trazamos una recta que pase por estos dos puntos.

No hay comentarios:
Publicar un comentario