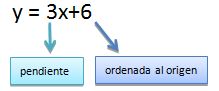
Además de las funciones lineales, uno de los tipos más comunes de funciones polinomiales con las que trabajamos en el álgebra es la función cuadrática. Una función cuadrática es una función que puede ser descrita por una ecuación de la forma y = ax2 + bx + c, donde a ≠ 0. Ningún término en la función polinomial tiene un grado mayor que 2. Las funciones cuadráticas son útiles cuando trabajamos con áreas, y frecuentemente aparecen en problemas de movimiento que implican gravedad o aceleración.
Las gráficas de las funciones cuadráticas tienen características que están estrechamente relacionadas con su forma simbólica. A medida que exploremos estas gráficas, aprenderemos a identificar estas características, y veremos algunas de las maneras de estructurar las ecuaciones cuadráticas.
Graficando con Puntos
Una función cuadrática es un polinomio de grado 2, es decir, el exponente más alto en la variable es 2. Los siguientes son ejemplos de funciones cuadráticas:
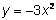
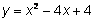
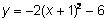
La función cuadrática más básica y simple tiene la ecuación
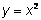. Si hacemos una tabla con los valores de esta función, vemos que el rango (los valores de y, o salida) no se comportan como una función lineal. En una función lineal, el valor de y cambia por la misma cantidad cada vez que el valor de x aumenta por 1. Eso no sucede con una función cuadrática:x
y = x2
-3
9
-2
4
-1
1
0
0
1
1
2
4
3
9
Los valores de y no cambian por una cantidad constante. Grafiquemos algunos puntos para ver cómo se vería la función:
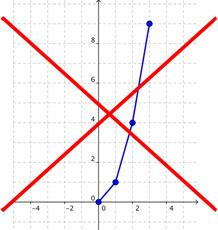
Después de graficar algunos puntos, podría ser tentador conectar los puntos con segmentos de línea, que son rectos. Pero esto estaría mal, y produciría un patrón que no representa la función.
Borremos esas líneas rectas y grafiquemos el resto de los puntos:
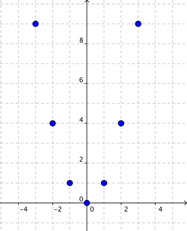
Ahora dibujamos una curva suave conectando los puntos.
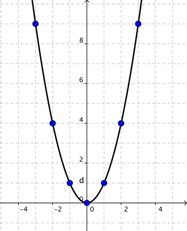
¡Mejor! Una función cuadrática resulta en una gráfica con forma de U, llamada parábola. Los valores de la función cambian suavemente, por lo que la curva debe ser suave también. Ahora que podemos ver la naturaleza de la parábola (forma de U), veamos su forma en detalle.
Características de una Parábola
La forma estándar de una ecuación cuadrática es
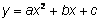. Por ejemplo 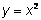, el valor del coeficiente a es 1, y b y c son 0. Si bien muchas ecuaciones cuadráticas presentan valores de b y c diferentes de cero, la gráfica resultante siempre será una parábola.Las parábolas tienen muchas propiedades que pueden ayudarnos a graficar ecuaciones cuadráticas. Una parábola tiene un punto especial llamado vértice; este es el punto donde la U "da la vuelta". Nota que en el vértice, la parábola cambia de dirección:
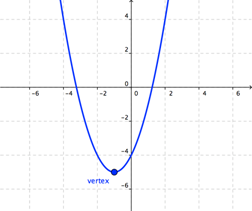
El vértice es el punto más alto o más bajo de la curva, dependiendo si la U se abre hacia arriba o hacia abajo. En el caso de que la parábola abra hacia arriba, el vértice será su punto más bajo; y una parábola que abre hacia abajo, tendrá un vértice en su punto más alto.
Todas las funciones parabólicas tienen un eje de simetría vertical, una línea imaginaria que pasa a través de la mitad de la forma de U y la divide en dos mitades que son imágenes de espejo una de la otra. El eje de simetría siempre pasa por el vértice. Cualquier par de puntos con el mismo valor de y estarán a la misma distancia del eje. En la gráfica interactiva siguiente, haz clic y arrastra el punto A y ve cómo se mueve el punto A'. Nota que el eje de simetría actúa como un espejo entre A y A’.
Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)
Dedica algún tiempo con la gráfica interactiva siguiente para que te familiarices con las parábolas y sus ecuaciones. Haz clic y arrastra los puntos, rojo, azul y verde para cambiar los valores de a, b, y c en la ecuación y = ax2 + bx + c, y observa qué pasa con la parábola.
Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)
Para la gráfica de una parábola, el primer coeficiente indica la dirección de la forma de U. Usa la gráfica interactiva y observa qué le pasa a la parábola con valores como a = 4 o a = -2. Verás que con valores positivos de a (a > 0), la parábola abre hacia arriba. Para valores negativos (a < 0), la parábola abre hacia abajo. También nota que cuando a = 0, la parábola ya no es una parábola, Se vuelve una línea recta, y la ecuación es ahora una ecuación lineal, y = bx + c.
Cuando a se aleja de 0 en cualquier dirección la parábola se vuelve más delgada. Consecuentemente, cuando a se acerca a 0, la parábola se hace más ancha (hasta que se convierte en una línea recta cuando a = 0). A veces comparamos una parábola con la gráfica de
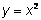. Cuando |a| > 1, la parábola es más ancha que 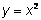y cuando |a| < 1, la parábola es más delgada que 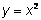. Intenta con la gráfica interactiva, usando valores como a = 2 o a = -3, y a = 0.2 o a = -0.4.¿Cuál de las siguientes ecuaciones cuadráticas es una parábola que abre hacia abajo?
1.
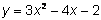
2.
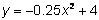
3.
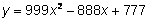
4.
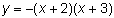
A) 1 y 3
B) 2 y 4
C) 3
D) 2
Mostrar/Ocultar la Respuesta
Graficando la Parábola usando el Vértice y el Eje de Simetría
Para una función cuadrática y = ax2 + bx + c, la coordenada x del vértice es siempre
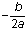. Como el eje de simetría siempre pasa por el vértice, significa que el eje de simetría es una línea vertical 
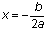. Cambia los valores de a y b en la gráfica siguiente para ver dónde están el vértice y la línea de simetría.Hemos visto cómo graficar una ecuación cuadrática dibujando los valores de x y y y conectándolos con una curva suave. Otra forma de graficar una parábola es usando lo que sabemos sobre el vértice y el eje de simetría. Sabemos que el vértice es el punto donde la parábola cambia de dirección. Y sabemos que cada punto de un lado del eje de simetría tiene un punto equivalente en el otro lado, a la misma distancia del eje y con la misma coordenada y. Si encontramos el vértice y algunos puntos de un lado, tendremos todo lo necesario para dibujar una gráfica.
Ejemplo
Problema
Usar el vértice y el eje de simetría para graficar
. 
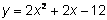Como el coeficientex2 es positivo, la parábola abre hacia arriba
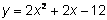
a = 2
b = 2
Para encontrar el vértice, encontrar los valores de a y b. Son los coeficientes de los términos x2 y xcuando la ecuación cuadrática se escribe en su forma estándar
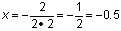
Encontrar la coordenada x del vértice sustituyendo los valores de a y ben la fórmula del vértice
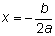
Encontrar la coordenada y del vértice sustituyendo el valor de x en la ecuación original
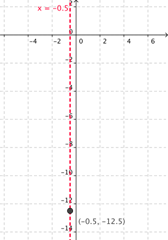
Graficar el vértice (-0.5, -12.5) y dibujar el eje de simetría x = -0.5.
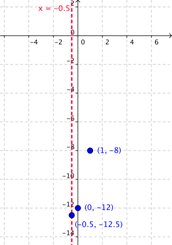
Graficar dos puntos en un lado del eje de simetría, como (0, -12) y (1, -8).
Nota: Podemos elegir cualquier valor de x que queramos; x = 0 y x = 1 son normalmente buenos porque los cálculos tienden a ser fáciles. Para encontrar los valores de y, sustituir los valores de x que hemos escogido en la función y resolverla
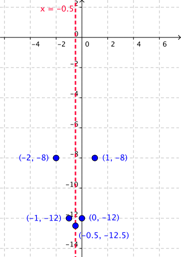
Dibujar los puntos correspondientes del otro lado del eje de simetría
Solución
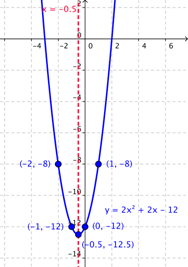
Terminar la parábola dibujando una curva suave que conecte todos los puntos
Factorizar para Encontrar las Raíces de una Parábola
Otras características útiles de una ecuación cuadrática son las raíces de una ecuación cuadrática. Las raíces son puntos donde la parábola toca o cruza el eje x. Las coordenadas x en esos puntos se conocen como intersección en x. (Las coordenadas y son 0.) Dependiendo de la naturaleza de la gráfica (la dirección de la forma de U y la localización del vértice), una función cuadrática puede tener cero, una, o dos raíces. Piensa por un momento sobre cómo se vería una parábola que intersecta el eje x en un solo lugar. O en dos lugares. ¿Cómo se vería una parábola que ni siquiera toca el eje x?
Aquí hay algunos ejemplos de parábolas con uno, dos y cero raíces.
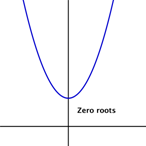
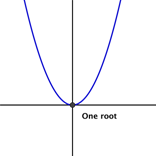
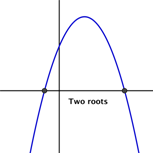
Para encontrar las raíces de una función cuadrática, podemos igualar la función a 0 (para que la coordenada y sea 0) y resolver la ecuación. Intentémoslo con una función cuadrática simple, con un coeficiente a = 1:
Ejemplo
Problema
Encontrar las raíces de
. 
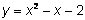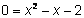
Como la intersección en xocurre cuando el valor de la coordenada y es igual a 0, encontramos las raíces igualando la ecuación a 0
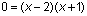
Factorizar
0 = x - 2
x = 2
0 = x + 1
x = -1
Usando la Propiedad Cero de la Multiplicacióntenemos que x – 2 = 0 o x + 1 = 0
Resolver ambas posibilidades
Solución
(2, 0) y (-1, 0)
Esta parábola tiene dos raíces
Gracias a la naturaleza simétrica de una parábola, si conocemos las raíces también podemos conocer la coordenada x del vértice. Si hay dos raíces, estará a la mitad entre ellas. En este caso, el vértice esta a una distancia igual entre x = 2 y x = -1, o en x = 0.5.
También podemos factorizar una ecuación cuadrática que tenga un coeficiente a diferente de 1:
Problema
Encontrar las raíces de
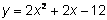
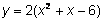
Empezar por sacar el factor común
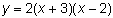
Factorizar el resto de la expresión
.
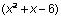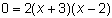
0 = x + 3 o 0 = x -2
Sustituir y por 0 y usar la Propiedad Cero de la Multiplicación.
Solución
(-3, 0) y (2, 0)
Esta parábola tiene dos raíces
La forma factorizada de una ecuación cuadrática también se le denomina forma intersección de una ecuación cuadrática. En esta forma,
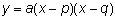, las intersecciones en x son p y q. Para una función que no tiene raíces, la ecuación no tiene forma intersección. Si la función tiene sólo una raíz, p = q y la forma intersección puede escribirse también como as y = a(x – p)2. Siempre y cuando una ecuación cuadrática pueda ser factorizada, podemos usar este método para encontrar las raíces.¿Cuál de las siguientes gráficas podrían representar la parábola dada por la ecuación cuadrática
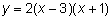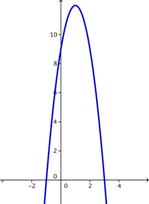
?A)
B)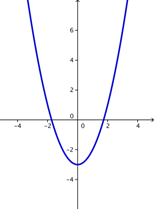
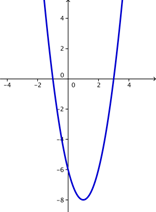
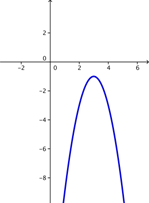
C) D)
A) Incorrecto. Esta parábola tiene las raíces correctas (3,0) y (-1, 0), pero la parábola abre hacia abajo. Como el coeficiente de x es 2, la parábola debería abrir hacia arriba. La respuesta correcta es C.
B) Incorrecto. Si bien esta parábola abre hacia arriba, las raíces no son (3, 0) y (-1, 0). La respuesta correcta es C.
C) Correcto. La gráfica muestra las raíces en (3, 0) y (-1, 0) y abre hacia arriba.
D) Incorrecto. Esta parábola no tiene raíces, pero la gráfica correcta debería tener dos raíces, (3, 0) y (-1, 0). Esta gráfica no tiene posibilidad de representar la ecuación. La respuesta correcta es C.
Sumario
La gráfica de una función cuadrática es una curva con forma de U llamada parábola. Puede ser trazada dibujando soluciones de la ecuación, encontrando el vértice y usando el eje de simetría para graficar puntos seleccionados, o encontrando las raíces y el vértice.
La forma estándar de una ecuación cuadrática es
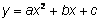. Esta forma nos permite encontrar fácilmente el vértice de la parábola y el eje de simetría usando la fórmula para la coordenada x del vértice, 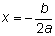.La forma intersección de una ecuación cuadrática es y =
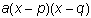. Las raíces, o intersecciones en x de la parábola son (p, 0) y (q, 0). No todas las ecuaciones cuadráticas tienen una intersección porque no todas las parábolas tienen una raíz.
